thus the playing style of different sides of conflict will be more diverse!
We will closely monitor the situation and collect the feedback.
Moving on to the next part of our blog! We would like to explain synergy earning and how it works depending on the strength of the enemy you killed. This table shows the levels of synergy for killed opponents, but do not forget - the more attention you give to being a team player and the objectives of the battle, the more synergy you get at the end of a battle!
In the final part of our blog, we would like to tell you about the mechanics of one of the types of our weapons - Gauss Cannon. We know that our pilots have rather lively discussions of the mechanics, and we would like to clarify what exactly is going on with damage calculation based on the number of weapons charges.
As you know, the more of this type of weapon charges, the greater the chance of dealing critical damage, however, critical damage itself is reduced in order to reduce the alpha strike strength. We have decided to use this mechanic to ensure that our players could inflict high damage, but did not destroy weak ships with single shots. More information can be found under the spoiler:
So, the basic formula for calculating weapon damage is as follows:
DMGfinal = X * DMGbasic * (1 + (A * X) * (B * / X))
Where X - is the number of charges.
DMGbasic - is the base damage of the gun.
A - Chance of dealing critical damage.
B - Critical damage value.
In the event of a critical hit, the formula becomes:
DMGfinal = X * DMGbasic * (1 +1 * (B / X))
Thus, if DMGbasic gun is 2000, we will see the following numbers on a crit with three charges:
DMGfinal = X * DMGbasic * (1 +1 * (B / X)) = 2000 * 3 * (1 * 0.1666666666666667 1) = 7000
However, when there’s no critical hit, we see the following:
DMGfinal = X * DMGbasic * (1 +0 * (B / X)) = X * DMG = 3 * 2000 * 1 = 6000.
Note: As you can see, X * A can not be greater than 1 (as it’s the probability of the event), so if you use the mechanics of charging and your chance of dealing critical damage exceeds 34%, then on the third charge you may lose some of your effective damage.
A simplified table for clarity:
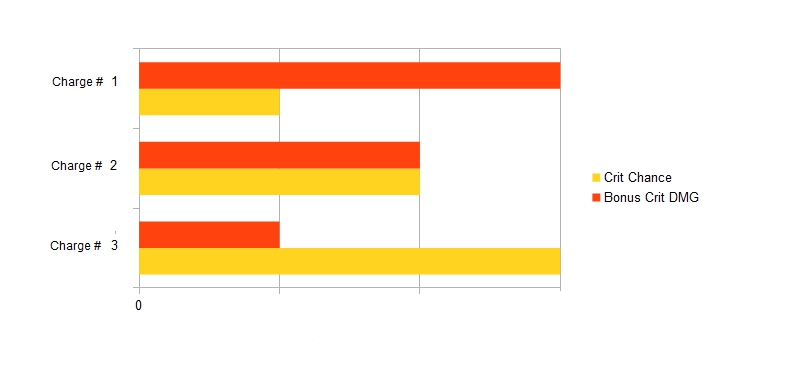
Thus, in order to increase the effectiveness of using this type of weapon, you can use the implants and modules that modify critical hit rates.
in fact, everyone will just play the ‘best in class’… ships will be even less varied. their stats may vary, but people will always choose one over the other for a given role.
yea… where have i heard that before…
synergy and DSR needs to grant a certain percent for assists. otherwise it leads to killstealing.
about the video - not sure what it shows except someone shooting an engineer 50 times to demonstrate how much it sucks.
and as for the calcs, appreciated, but all you’ve done is demonstrate once again, how inferior it is to other guns.
even if you MISS half your shots with a railgun, you still get the same DPS as a gauss.
and since when do gauss do 2000 damage per shot? they do 1000…
so your ‘theoretical’ alpha damage there is actually 4000, not 7000… reduced by resistances = 2500-3000 damage… that’s not alpha… that’s a joke…
a single singularity shot will do more damage than that when it crits: 5000+, so 3000-3500 after resistances…
and the dps is not even comparable… as i said… half the DPS… you can miss half your shots with other guns and still come out on top.
also, your math is incorrect:
DMGfinal = X * DMGbasic * (1 + (A * X) * (B * / X))
(B * / X) is denoted (B / X) below.
Where X - is the number of charges.
DMGbasic - is the base damage of the gun.
A - Chance of dealing critical damage.
B - Critical damage value.
In the event of a critical hit, the formula becomes:
DMGfinal = X * DMGbasic * (1 +1 * (B / X))
Thus, if DMGbasic gun is 2000, we will see the following numbers on a crit with three charges:
DMGfinal = X * DMGbasic * (1 +1 * (B / X)) = 2000 * 3 * (1 * 0.1666666666666667 1) = 7000
However, when there’s no critical hit, we see the following:
DMGfinal = X * DMGbasic * (1 +0 * (B / X)) = X * DMG = 3 * 2000 * 1 = 6000.
finally: DMGfinal = X * DMGbasic * (1 + (A * X) * (B / X))
DMGfinal = 3 * 1000 * (1 + (1 * 3) * (1 / 3))
DMGfinal = 3000 * (1 + (3) * (1/3))
DMGfinal = 3000 * (1 + 1)
DMGfinal = 3000 * 2
DMGfinal = 6000
so your formula doesn’t add up with what you are saying… what it actually depicts is crits applying to all 3 shots.
if you replace the (A * X) with just A (crit chance) then it does match up with what you’re saying, if you let A = 1 when a crit occurs and A = 0 when it doesn’t. ie:
DMGfinal = X * DMGbasic * (1 + A * (B / X))
DMGfinal = 3 * 1000 * (1 + 1 * (1 / 6))
DMGfinal = 3000 * (7 / 6)
DMGfinal = 3500
in fact, as soon as you include crit chance as a percentage, you are no longer calculating damage per shot, but DPS (or average damage per shot)
and what happens when crits chance is greater than 33.33% ? the value of (A * X) will be greater than 1… :\ if you have crit rate 0.95 * 3 = 2.85… it’ll throw the math way off.
but yea, in fact if you have crits higher than 33%, you are wasting it by charging the gun… firing every shot will net more crit damage.
 No cap problems taht I can see, dunno what the moan is all about.
No cap problems taht I can see, dunno what the moan is all about.
